Welcome to arithmeticcurve’s documentation!¶
This module calculates an arithmetic mean curve in regard of the described algorithm in (Scheliga 2013).
Warning
This module is at a beta development state. With future releases the wording (function, attribute and class names) may change towards a more common understanding.
Current main construction parts are additional tests of this package.
Contents:
Example sample curves¶
The figure 1 shows an exemplary sample of curves with the mean values along the sample. The character of calculating the mean value without an extrapolation is observable by a mean curve jumping to different mean states, when the amount of available values change.
(Source code, png, hires.png, pdf)
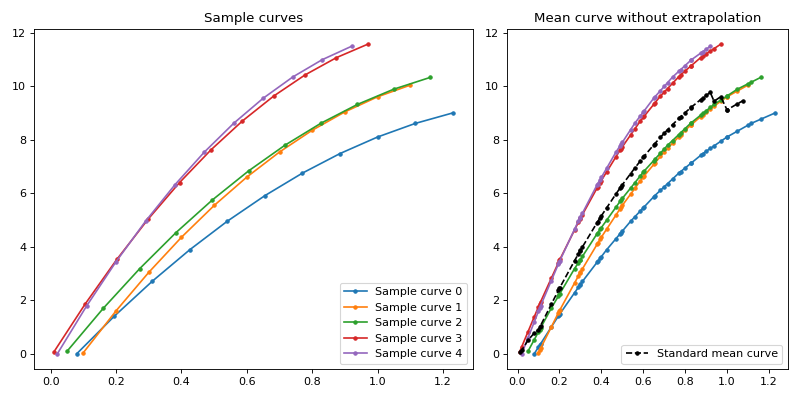
Figure 1: Sample curves (left) and with standard mean curve (right).
Prerequisites of calculation¶
The curves must be a pandas.DataFrame with the x-value being the index.
The index (x-values) of the curves must be monotonic increasing and must not contain duplicates.
pandas.MultiIndex is not supported.
Arithmetic mean curve¶
The figure 2 shows a mean curve based on the concept described in (Scheliga 2013). The arithmetic mean curve is calculated by extrapolating the curves on the base of their relative position within the standard deviation at the point the first curve ended. The extrapolation is based on an iterative process, in which the extrapolated mean value and extrapolated single curve(s) reach an asymptote. The calculated arithmetic curve does not intentionally extrapolate the beginning of the sample curves, starting at the first full definition of all sample curves (figure 3). Prior calculation of the arithmetic mean curve the single supplied curves should be prepared.
The scatter band is the representation of the standard deviation around the mean curve. Its end is sheared in accordance to the mean curves ending slope, as the std circle indicates.
(Source code, png, hires.png, pdf)
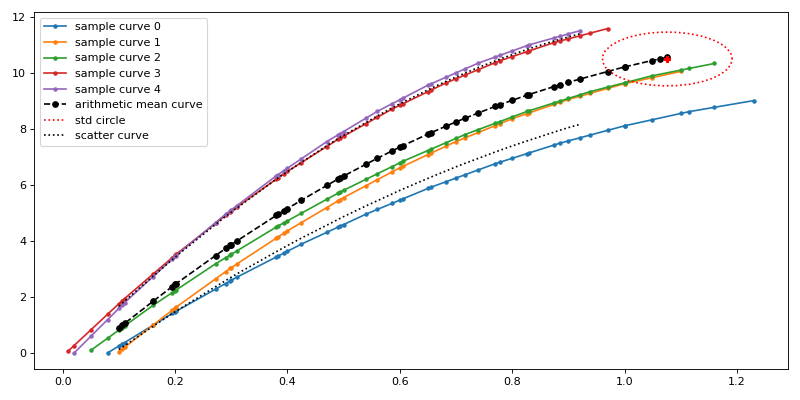
Figure 2: Extrapolated mean curve with scatter curve (Scheliga 2013)
(Source code, png, hires.png, pdf)
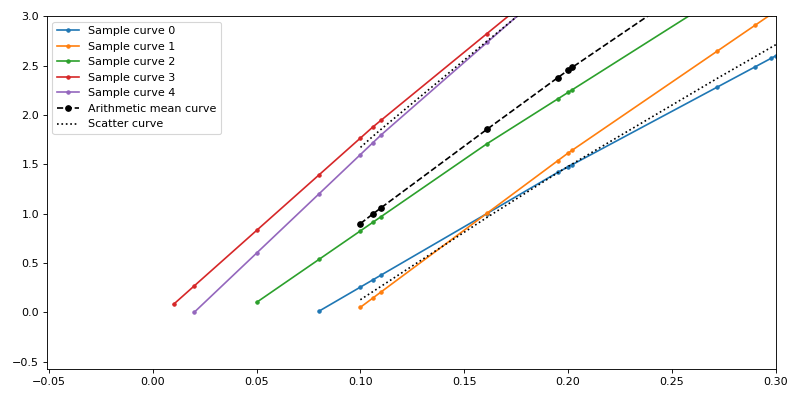
Figure 3: Sample curves left sides with arithmetic mean curve.
References¶
D. Scheliga, Experimentelle Untersuchung des Rissausbreitungsverhaltens von nanopartikelverstärktem Polyamid 66. Kaiserslautern: Institut für Verbundwerkstoffe GmbH, 2013, ISBN 978-2-944440-02-6